This is a Jupyter Notebook for experimenting with different supervised learning estimators offered by SciKit Learn to determine which one performs better for the given data set with hyperparameter tuning.
The following Python support classes are used in this notebook:
Exploratory Data Analysis Python Module
Modeling Training Python Module
Business Goal
To predict the concrete strength using the data available in file "concrete.csv". Apply feature engineering and model tuning to obtain a score above 85%.
NOTE: Comments on the results of all aspects of this work are found in the Summary of Results section at the end of this notebook.
In [93]:
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from ExploratoryDataAnalysis import ExploratoryDataAnalysis
from ModelTraining import ModelTraining
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
from sklearn.ensemble import GradientBoostingRegressor, RandomForestRegressor
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
%matplotlib inline
import warnings
Explore Data¶
In [2]:
warnings.filterwarnings('ignore')
In [3]:
%%javascript
IPython.OutputArea.auto_scroll_threshold = 9999;
In [4]:
data = pd.read_csv("concrete.csv")
preparedData1 = data.copy()
preparedData2 = data.copy()
preparedData3 = data.copy()
preparedData4 = data.copy()
preparedData5 = data.copy()
In [5]:
data.head()
Out[5]:
| cement | slag | ash | water | superplastic | coarseagg | fineagg | age | strength | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 141.3 | 212.0 | 0.0 | 203.5 | 0.0 | 971.8 | 748.5 | 28 | 29.89 |
| 1 | 168.9 | 42.2 | 124.3 | 158.3 | 10.8 | 1080.8 | 796.2 | 14 | 23.51 |
| 2 | 250.0 | 0.0 | 95.7 | 187.4 | 5.5 | 956.9 | 861.2 | 28 | 29.22 |
| 3 | 266.0 | 114.0 | 0.0 | 228.0 | 0.0 | 932.0 | 670.0 | 28 | 45.85 |
| 4 | 154.8 | 183.4 | 0.0 | 193.3 | 9.1 | 1047.4 | 696.7 | 28 | 18.29 |
In [6]:
data.shape
Out[6]:
(1030, 9)
In [7]:
data.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 1030 entries, 0 to 1029 Data columns (total 9 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 cement 1030 non-null float64 1 slag 1030 non-null float64 2 ash 1030 non-null float64 3 water 1030 non-null float64 4 superplastic 1030 non-null float64 5 coarseagg 1030 non-null float64 6 fineagg 1030 non-null float64 7 age 1030 non-null int64 8 strength 1030 non-null float64 dtypes: float64(8), int64(1) memory usage: 72.5 KB
In [8]:
data.describe().T
Out[8]:
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| cement | 1030.0 | 281.167864 | 104.506364 | 102.00 | 192.375 | 272.900 | 350.000 | 540.0 |
| slag | 1030.0 | 73.895825 | 86.279342 | 0.00 | 0.000 | 22.000 | 142.950 | 359.4 |
| ash | 1030.0 | 54.188350 | 63.997004 | 0.00 | 0.000 | 0.000 | 118.300 | 200.1 |
| water | 1030.0 | 181.567282 | 21.354219 | 121.80 | 164.900 | 185.000 | 192.000 | 247.0 |
| superplastic | 1030.0 | 6.204660 | 5.973841 | 0.00 | 0.000 | 6.400 | 10.200 | 32.2 |
| coarseagg | 1030.0 | 972.918932 | 77.753954 | 801.00 | 932.000 | 968.000 | 1029.400 | 1145.0 |
| fineagg | 1030.0 | 773.580485 | 80.175980 | 594.00 | 730.950 | 779.500 | 824.000 | 992.6 |
| age | 1030.0 | 45.662136 | 63.169912 | 1.00 | 7.000 | 28.000 | 56.000 | 365.0 |
| strength | 1030.0 | 35.817961 | 16.705742 | 2.33 | 23.710 | 34.445 | 46.135 | 82.6 |
In [9]:
numericalFeatures = ["cement", "slag", "ash", "water", "superplastic", "coarseagg", "fineagg", "age"]
categoricalFeatures = []
In [10]:
eda = ExploratoryDataAnalysis(data)
# setting up the EDA object with key data that can then be used in support of its other method calls
eda.setNumericalFeatures(numericalFeatures)
eda.setCategoricalFeatures(categoricalFeatures)
eda.setTargetFeature("strength", False)
In [11]:
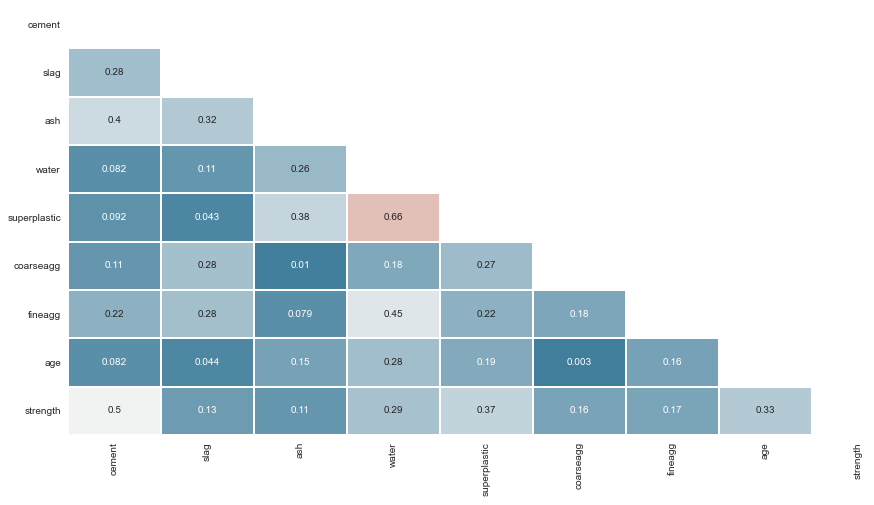
eda.plotCorrelations()
In [12]:
eda.VIFSummary().sort_values(by=["VIF"], ascending=False)
Out[12]:
| Feature | VIF | |
|---|---|---|
| 5 | coarseagg | 84.955779 |
| 3 | water | 82.157569 |
| 6 | fineagg | 72.790995 |
| 0 | cement | 15.456717 |
| 4 | superplastic | 5.471094 |
| 2 | ash | 4.147833 |
| 1 | slag | 3.329127 |
| 7 | age | 1.699459 |
In [13]:
eda.analyzeSkew().sort_values(by=['OriginalSkew'], ascending=False)
Out[13]:
| OriginalSkew | LnSkew | SqRtSkew | |
|---|---|---|---|
| age | 3.269177 | -0.005085 | 1.618107 |
| superplastic | 0.907203 | -0.324821 | 0.066247 |
| slag | 0.800717 | -0.032700 | 0.306931 |
| ash | 0.537354 | 0.226638 | 0.325631 |
| cement | 0.509481 | -0.127149 | 0.191411 |
| water | 0.074628 | -0.303418 | -0.112604 |
| coarseagg | -0.040220 | -0.209827 | -0.124750 |
| fineagg | -0.253010 | -0.539191 | -0.396633 |
In [14]:
eda.analyzeNumericalFeature("age", True)
age -- Numerical Feature Analysis
Summary
|
|
|
Notes
TODOPlots with Numerical Features
In [15]:
eda.generateNumericalBinsTable("age", 20).sort_index()
Out[15]:
1.0 322 19.2 425 37.4 0 55.599999999999994 91 73.8 76 92.0 52 110.19999999999999 3 128.39999999999998 0 146.6 0 164.79999999999998 26 183.0 0 201.2 0 219.39999999999998 0 237.6 0 255.79999999999998 13 274.0 0 292.2 0 310.4 0 328.59999999999997 0 346.8 20 Name: age-bin, dtype: int64
In [16]:
data[data["age"] == 28]["age"].value_counts().sort_index()
Out[16]:
28 425 Name: age, dtype: int64
In [17]:
data[data["age"] < 28]["age"].value_counts().sort_index()
Out[17]:
1 2 3 134 7 126 14 62 Name: age, dtype: int64
In [18]:
data[data["age"] > 28]["age"].value_counts().sort_index()
Out[18]:
56 91 90 54 91 22 100 52 120 3 180 26 270 13 360 6 365 14 Name: age, dtype: int64
In [19]:
eda.analyzeNumericalFeature("superplastic", True)
superplastic -- Numerical Feature Analysis
Summary
|
|
|
Notes
TODOPlots with Numerical Features
In [20]:
eda.analyzeNumericalFeature("slag", True)
slag -- Numerical Feature Analysis
Summary
|
|
|
Notes
TODOPlots with Numerical Features
In [21]:
eda.analyzeNumericalFeature("ash", True)
ash -- Numerical Feature Analysis
Summary
|
|
|
Notes
TODOPlots with Numerical Features
In [22]:
eda.analyzeNumericalFeature("cement", True)
cement -- Numerical Feature Analysis
Summary
|
|
|
Notes
TODOPlots with Numerical Features
In [23]:
eda.analyzeNumericalFeature("water", True)
water -- Numerical Feature Analysis
Summary
|
|
|
Notes
TODOPlots with Numerical Features
In [24]:
eda.analyzeNumericalFeature("coarseagg", True)
coarseagg -- Numerical Feature Analysis
Summary
|
|
|
Notes
TODOPlots with Numerical Features
In [25]:
eda.analyzeNumericalFeature("fineagg", True)
fineagg -- Numerical Feature Analysis
Summary
|
|
|
Notes
TODOPlots with Numerical Features
Model Training Iteration 1¶
Prepare Data¶
In [26]:
x1 = preparedData1.loc[:, preparedData1.columns != 'strength'] # independent variables
y1 = preparedData1.loc[:, preparedData1.columns == 'strength'] # Target variable
In [27]:
y1.head(5)
Out[27]:
| strength | |
|---|---|
| 0 | 29.89 |
| 1 | 23.51 |
| 2 | 29.22 |
| 3 | 45.85 |
| 4 | 18.29 |
In [28]:
x1train,x1test,y1train,y1test = train_test_split(x1,y1,test_size=0.3,random_state=10)
Train Models¶
In [29]:
modelTraining1 = ModelTraining(x1train, x1test, y1train, y1test)
cvResults1 = modelTraining1.crossValidationForNumericalTarget(x1train, y1train, 4)
Compare Results¶
In [30]:
cvResults1
Out[30]:
| Model Name | Fold Number | Mean Absolute Error | Root Mean Squared Error | R Squared | |
|---|---|---|---|---|---|
| 0 | Linear Regressor | 1 | 7.812667 | 9.982897 | 0.672115 |
| 1 | Linear Regressor | 2 | 7.718038 | 9.909330 | 0.669944 |
| 2 | Linear Regressor | 3 | 7.720803 | 9.802753 | 0.576401 |
| 3 | Linear Regressor | 4 | 8.599319 | 11.114082 | 0.596190 |
| 4 | Bagging Regressor | 1 | 7.797968 | 9.984500 | 0.672010 |
| 5 | Bagging Regressor | 2 | 7.739220 | 9.912804 | 0.669713 |
| 6 | Bagging Regressor | 3 | 7.738692 | 9.809792 | 0.575793 |
| 7 | Bagging Regressor | 4 | 8.593172 | 11.085801 | 0.598243 |
| 8 | Adaptive Boosting Regressor | 1 | 8.035515 | 10.248558 | 0.654432 |
| 9 | Adaptive Boosting Regressor | 2 | 7.846824 | 9.989964 | 0.664551 |
| 10 | Adaptive Boosting Regressor | 3 | 7.782421 | 9.702993 | 0.584979 |
| 11 | Adaptive Boosting Regressor | 4 | 8.661681 | 11.150640 | 0.593530 |
| 12 | Random Forest Regressor | 1 | 3.727772 | 5.044952 | 0.916262 |
| 13 | Random Forest Regressor | 2 | 4.062766 | 5.458071 | 0.899867 |
| 14 | Random Forest Regressor | 3 | 4.056850 | 5.665687 | 0.858498 |
| 15 | Random Forest Regressor | 4 | 4.201580 | 5.932129 | 0.884960 |
| 16 | Decision Tree Regressor | 1 | 7.081140 | 9.457873 | 0.705697 |
| 17 | Decision Tree Regressor | 2 | 5.895200 | 8.032594 | 0.783125 |
| 18 | Decision Tree Regressor | 3 | 6.723521 | 8.735725 | 0.663600 |
| 19 | Decision Tree Regressor | 4 | 7.070700 | 8.805911 | 0.746500 |
| 20 | Gradient Boosting Regressor | 1 | 4.296660 | 5.464380 | 0.901760 |
| 21 | Gradient Boosting Regressor | 2 | 4.596520 | 5.960752 | 0.880574 |
| 22 | Gradient Boosting Regressor | 3 | 4.363445 | 5.950663 | 0.843905 |
| 23 | Gradient Boosting Regressor | 4 | 5.072889 | 6.753827 | 0.850882 |
In [31]:
stats1 = cvResults1.drop("Mean Absolute Error", axis=1).drop("Root Mean Squared Error", axis=1).groupby('Model Name').describe()
stats1
Out[31]:
| R Squared | ||||||||
|---|---|---|---|---|---|---|---|---|
| count | mean | std | min | 25% | 50% | 75% | max | |
| Model Name | ||||||||
| Adaptive Boosting Regressor | 4.0 | 0.624373 | 0.040911 | 0.584979 | 0.591392 | 0.623981 | 0.656962 | 0.664551 |
| Bagging Regressor | 4.0 | 0.628940 | 0.049276 | 0.575793 | 0.592630 | 0.633978 | 0.670287 | 0.672010 |
| Decision Tree Regressor | 4.0 | 0.724730 | 0.051585 | 0.663600 | 0.695172 | 0.726098 | 0.755656 | 0.783125 |
| Gradient Boosting Regressor | 4.0 | 0.869280 | 0.026863 | 0.843905 | 0.849138 | 0.865728 | 0.885870 | 0.901760 |
| Linear Regressor | 4.0 | 0.628663 | 0.049592 | 0.576401 | 0.591243 | 0.633067 | 0.670487 | 0.672115 |
| Random Forest Regressor | 4.0 | 0.889897 | 0.024528 | 0.858498 | 0.878344 | 0.892413 | 0.903966 | 0.916262 |
In [32]:
plt.figure(figsize=(15, 6))
sns.boxplot(x="Model Name", y="R Squared", data=cvResults1)
Out[32]:
<AxesSubplot:xlabel='Model Name', ylabel='R Squared'>
In [33]:
modelTraining1.estimateNumericalFeatureImportance().sort_values(by="Coefficient", ascending=False)
Out[33]:
| Feature | Coefficient | |
|---|---|---|
| 4 | superplastic | 0.391480 |
| 7 | age | 0.125095 |
| 0 | cement | 0.120832 |
| 1 | slag | 0.110053 |
| 2 | ash | 0.083132 |
| 5 | coarseagg | 0.025016 |
| 6 | fineagg | 0.024993 |
| 3 | water | -0.117713 |
Model Training Iteration 2¶
Prepare Data¶
In [34]:
preparedData2["cement 2 water"] = preparedData2["cement"] / preparedData2["water"]
In [35]:
preparedData2.drop("cement", axis=1, inplace=True)
preparedData2.drop("water", axis=1, inplace=True)
In [36]:
bins = [0, 1, 3, 7, 14, 28, 365]
bin_labels = [1, 3, 7, 14, 28, 365]
preparedData2["age-bin"] = pd.cut(x=preparedData2["age"], bins=bins, labels=bin_labels)
In [37]:
preparedData2["age-bin"].value_counts()
Out[37]:
28 425 365 281 3 134 7 126 14 62 1 2 Name: age-bin, dtype: int64
In [38]:
preparedData2.drop("age", axis=1, inplace=True)
In [39]:
preparedData2 = pd.get_dummies(preparedData2)
In [40]:
preparedData2.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 1030 entries, 0 to 1029 Data columns (total 13 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 slag 1030 non-null float64 1 ash 1030 non-null float64 2 superplastic 1030 non-null float64 3 coarseagg 1030 non-null float64 4 fineagg 1030 non-null float64 5 strength 1030 non-null float64 6 cement 2 water 1030 non-null float64 7 age-bin_1 1030 non-null uint8 8 age-bin_3 1030 non-null uint8 9 age-bin_7 1030 non-null uint8 10 age-bin_14 1030 non-null uint8 11 age-bin_28 1030 non-null uint8 12 age-bin_365 1030 non-null uint8 dtypes: float64(7), uint8(6) memory usage: 62.5 KB
In [41]:
x2 = preparedData2.loc[:, preparedData2.columns != 'strength'] # independent variables
y2 = preparedData2.loc[:, preparedData2.columns == 'strength'] # Target variable
In [42]:
x2train,x2test,y2train,y2test = train_test_split(x2,y2,test_size=0.3,random_state=10)
Train Models¶
In [43]:
modelTraining2 = ModelTraining(x2train, x2test, y2train, y2test)
cvResults2 = modelTraining2.crossValidationForNumericalTarget(x2train, y2train, 4)
Compare Models¶
In [44]:
stats2 = cvResults2.groupby('Model Name').describe()
stats2.T
Out[44]:
| Model Name | Adaptive Boosting Regressor | Bagging Regressor | Decision Tree Regressor | Gradient Boosting Regressor | Linear Regressor | Random Forest Regressor | |
|---|---|---|---|---|---|---|---|
| Mean Absolute Error | count | 4.000000 | 4.000000 | 4.000000 | 4.000000 | 4.000000 | 4.000000 |
| mean | 5.775960 | 5.640702 | 6.422270 | 4.422064 | 5.611743 | 4.076853 | |
| std | 0.448044 | 0.477285 | 0.193601 | 0.284635 | 0.458426 | 0.260819 | |
| min | 5.304164 | 5.173187 | 6.279967 | 4.100542 | 5.165341 | 3.800593 | |
| 25% | 5.452492 | 5.263840 | 6.322060 | 4.266870 | 5.244067 | 3.898220 | |
| 50% | 5.767930 | 5.630234 | 6.350667 | 4.405926 | 5.614883 | 4.062989 | |
| 75% | 6.091398 | 6.007096 | 6.450877 | 4.561120 | 5.982559 | 4.241621 | |
| max | 6.263817 | 6.129154 | 6.707779 | 4.775861 | 6.051864 | 4.380840 | |
| Root Mean Squared Error | count | 4.000000 | 4.000000 | 4.000000 | 4.000000 | 4.000000 | 4.000000 |
| mean | 7.353605 | 7.245583 | 8.511871 | 5.716413 | 7.217221 | 5.676794 | |
| std | 0.555766 | 0.522131 | 0.443730 | 0.436197 | 0.502604 | 0.621228 | |
| min | 6.914904 | 6.765523 | 8.107791 | 5.413031 | 6.755990 | 5.146633 | |
| 25% | 6.919835 | 6.837295 | 8.281056 | 5.506826 | 6.814926 | 5.180930 | |
| 50% | 7.210220 | 7.178639 | 8.399732 | 5.544286 | 7.163887 | 5.562069 | |
| 75% | 7.643990 | 7.586927 | 8.630546 | 5.753873 | 7.566183 | 6.057933 | |
| max | 8.079076 | 7.859530 | 9.140230 | 6.364047 | 7.785120 | 6.436408 | |
| R Squared | count | 4.000000 | 4.000000 | 4.000000 | 4.000000 | 4.000000 | 4.000000 |
| mean | 0.807449 | 0.813295 | 0.740333 | 0.883137 | 0.814730 | 0.882924 | |
| std | 0.024609 | 0.020600 | 0.044193 | 0.019628 | 0.020153 | 0.033560 | |
| min | 0.786620 | 0.798060 | 0.684452 | 0.864799 | 0.798796 | 0.844894 | |
| 25% | 0.788570 | 0.798186 | 0.716278 | 0.866898 | 0.801098 | 0.859651 | |
| 50% | 0.802101 | 0.806677 | 0.746580 | 0.883118 | 0.808567 | 0.886974 | |
| 75% | 0.820981 | 0.821786 | 0.770636 | 0.899358 | 0.822199 | 0.910247 | |
| max | 0.838974 | 0.841766 | 0.783722 | 0.901513 | 0.842992 | 0.912853 |
In [45]:
poly = modelTraining2.findOptimalPolynomialDegree(x2train, y2train)
In [46]:
sns.regplot(data=poly, y="Root Mean Squared Error", x="Degree", order=2)
Out[46]:
<AxesSubplot:xlabel='Degree', ylabel='Root Mean Squared Error'>
In [47]:
modelTraining2.crossValidationForPolynomialModel(x2train, y2train, 4, 2)
Out[47]:
| Model Name | Fold Number | Mean Absolute Error | Root Mean Squared Error | |
|---|---|---|---|---|
| 0 | Polynomial Regressor | 1 | 4.743177 | 6.108623 |
| 1 | Polynomial Regressor | 2 | 4.520351 | 5.968825 |
| 2 | Polynomial Regressor | 3 | 4.601101 | 6.146301 |
| 3 | Polynomial Regressor | 4 | 5.481640 | 7.318558 |
In [48]:
poly.groupby('Degree').describe().T
Out[48]:
| Degree | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | |
|---|---|---|---|---|---|---|---|---|---|
| Mean Absolute Error | count | 4.000000 | 4.000000 | 4.000000 | 4.000000 | 4.000000e+00 | 4.000000e+00 | 4.000000e+00 | 4.000000e+00 |
| mean | 4.836567 | 8.325034 | 19093.011324 | 2907.544183 | 1.185340e+05 | 7.764696e+05 | 5.111988e+05 | 4.834760e+05 | |
| std | 0.439802 | 4.279830 | 18930.113476 | 4131.759665 | 1.583133e+05 | 1.112365e+06 | 5.864299e+05 | 4.904486e+05 | |
| min | 4.520351 | 5.332594 | 410.484645 | 40.001544 | 2.942298e+03 | 5.402570e+04 | 5.950779e+04 | 5.913931e+04 | |
| 25% | 4.580913 | 5.497082 | 10863.354537 | 192.080333 | 9.786127e+03 | 6.406995e+04 | 7.158651e+04 | 7.232251e+04 | |
| 50% | 4.672139 | 6.733463 | 15253.886935 | 1354.052651 | 6.398463e+04 | 3.239119e+05 | 3.404718e+05 | 4.258779e+05 | |
| 75% | 4.927792 | 9.561414 | 23483.543722 | 4069.516501 | 1.727325e+05 | 1.036312e+06 | 7.800841e+05 | 8.370314e+05 | |
| max | 5.481640 | 14.500616 | 45453.786781 | 8882.069884 | 3.432245e+05 | 2.404029e+06 | 1.304344e+06 | 1.023009e+06 | |
| Root Mean Squared Error | count | 4.000000 | 4.000000 | 4.000000 | 4.000000 | 4.000000e+00 | 4.000000e+00 | 4.000000e+00 | 4.000000e+00 |
| mean | 6.385577 | 32.563230 | 144590.965779 | 21293.723393 | 1.139116e+06 | 6.985638e+06 | 4.445018e+06 | 4.297793e+06 | |
| std | 0.626656 | 35.746829 | 162182.257887 | 30204.300518 | 1.758145e+06 | 1.041769e+07 | 5.380645e+06 | 4.351111e+06 | |
| min | 5.968825 | 7.751987 | 3523.091590 | 352.315363 | 2.707856e+04 | 5.289558e+05 | 5.836529e+05 | 5.877440e+05 | |
| 25% | 6.073674 | 10.723495 | 66082.831713 | 1425.117128 | 7.291899e+04 | 6.723278e+05 | 7.402828e+05 | 7.524689e+05 | |
| 50% | 6.127462 | 18.802549 | 98418.419712 | 9928.064467 | 3.966873e+05 | 2.509711e+06 | 2.548713e+06 | 3.568028e+06 | |
| 75% | 6.439365 | 40.642284 | 176926.553778 | 29796.670732 | 1.462884e+06 | 8.823021e+06 | 6.253449e+06 | 7.113352e+06 | |
| max | 7.318558 | 84.895836 | 378003.932104 | 64966.449276 | 3.736010e+06 | 2.239417e+07 | 1.209899e+07 | 9.467372e+06 |
In [49]:
plt.figure(figsize=(15, 6))
sns.boxplot(x="Model Name", y="R Squared", data=cvResults2);
In [50]:
modelTraining2.estimateNumericalFeatureImportance().sort_values(by="Coefficient", ascending=False)
Out[50]:
| Feature | Coefficient | |
|---|---|---|
| 11 | age-bin_365 | 20.776766 |
| 5 | cement 2 water | 19.693523 |
| 10 | age-bin_28 | 9.644236 |
| 9 | age-bin_14 | 6.284208 |
| 0 | slag | 0.087340 |
| 1 | ash | 0.058530 |
| 3 | coarseagg | 0.012178 |
| 4 | fineagg | 0.003425 |
| 2 | superplastic | -0.019066 |
| 8 | age-bin_7 | -4.131992 |
| 7 | age-bin_3 | -9.357011 |
| 6 | age-bin_1 | -23.216206 |
Feature Engineering Performance Improvement Analysis¶
Cement / Water Replaces Cement and Water¶
In [51]:
preparedData3["cement 2 water"] = preparedData3["cement"] / preparedData3["water"]
preparedData3.drop("cement", axis=1, inplace=True)
preparedData3.drop("water", axis=1, inplace=True)
x3 = preparedData3.loc[:, preparedData3.columns != 'strength'] # independent variables
y3 = preparedData3.loc[:, preparedData3.columns == 'strength'] # Target variable
x3train,x3test,y3train,y3test = train_test_split(x3,y3,test_size=0.3,random_state=10)
modelTraining3 = ModelTraining(x3train, x3test, y3train, y3test)
cvResults3 = modelTraining3.crossValidationForNumericalTarget(x3train, y3train, 4)
stats3 = cvResults3.drop("Mean Absolute Error", axis=1).drop("Root Mean Squared Error", axis=1).groupby('Model Name').describe()
stats3
Out[51]:
| R Squared | ||||||||
|---|---|---|---|---|---|---|---|---|
| count | mean | std | min | 25% | 50% | 75% | max | |
| Model Name | ||||||||
| Adaptive Boosting Regressor | 4.0 | 0.620606 | 0.038680 | 0.574792 | 0.598909 | 0.621276 | 0.642973 | 0.665082 |
| Bagging Regressor | 4.0 | 0.626045 | 0.041920 | 0.572767 | 0.604924 | 0.630666 | 0.651788 | 0.670082 |
| Decision Tree Regressor | 4.0 | 0.769368 | 0.058768 | 0.691539 | 0.747113 | 0.776917 | 0.799172 | 0.832098 |
| Gradient Boosting Regressor | 4.0 | 0.871168 | 0.024361 | 0.842774 | 0.855079 | 0.873897 | 0.889987 | 0.894105 |
| Linear Regressor | 4.0 | 0.626075 | 0.041896 | 0.572793 | 0.604883 | 0.630826 | 0.652018 | 0.669856 |
| Random Forest Regressor | 4.0 | 0.899372 | 0.029898 | 0.858853 | 0.886017 | 0.906970 | 0.920325 | 0.924694 |
Age Bins Hot One Encoding Replaces Continuous Age Numerical Feature¶
In [52]:
bins = [0, 1, 3, 7, 14, 28, 365]
bin_labels = [1, 3, 7, 14, 28, 365]
preparedData4["age-bin"] = pd.cut(x=preparedData4["age"], bins=bins, labels=bin_labels)
preparedData4.drop("age", axis=1, inplace=True)
x4 = preparedData4.loc[:, preparedData4.columns != 'strength'] # independent variables
y4 = preparedData4.loc[:, preparedData4.columns == 'strength'] # Target variable
x4train,x4test,y4train,y4test = train_test_split(x4,y4,test_size=0.3,random_state=10)
modelTraining4 = ModelTraining(x4train, x4test, y4train, y4test)
cvResults4 = modelTraining4.crossValidationForNumericalTarget(x4train, y4train, 4)
stats4 = cvResults4.drop("Mean Absolute Error", axis=1).drop("Root Mean Squared Error", axis=1).groupby('Model Name').describe()
stats4
Out[52]:
| R Squared | ||||||||
|---|---|---|---|---|---|---|---|---|
| count | mean | std | min | 25% | 50% | 75% | max | |
| Model Name | ||||||||
| Adaptive Boosting Regressor | 4.0 | 0.681535 | 0.023550 | 0.652932 | 0.673305 | 0.681323 | 0.689554 | 0.710563 |
| Bagging Regressor | 4.0 | 0.682640 | 0.025406 | 0.653693 | 0.671510 | 0.680761 | 0.691891 | 0.715343 |
| Decision Tree Regressor | 4.0 | 0.724730 | 0.051585 | 0.663600 | 0.695172 | 0.726098 | 0.755656 | 0.783125 |
| Gradient Boosting Regressor | 4.0 | 0.876297 | 0.017845 | 0.856792 | 0.863344 | 0.878182 | 0.891134 | 0.892030 |
| Linear Regressor | 4.0 | 0.682481 | 0.024782 | 0.655226 | 0.670326 | 0.679949 | 0.692104 | 0.714802 |
| Random Forest Regressor | 4.0 | 0.888737 | 0.025498 | 0.857692 | 0.874372 | 0.890501 | 0.904865 | 0.916253 |
Compare the Performance of All Four Feature Sets¶
In [53]:
featureCompare = pd.DataFrame()
featureCompare["Original"] = stats1[('R Squared', 'mean')]
featureCompare["Age Bins and Cement/Water"] = stats2[('R Squared', 'mean')]
featureCompare["Only Cement/Water"] = stats3[('R Squared', 'mean')]
featureCompare["Only Age Bins"] = stats4[('R Squared', 'mean')]
featureCompare
Out[53]:
| Original | Age Bins and Cement/Water | Only Cement/Water | Only Age Bins | |
|---|---|---|---|---|
| Model Name | ||||
| Adaptive Boosting Regressor | 0.624373 | 0.807449 | 0.620606 | 0.681535 |
| Bagging Regressor | 0.628940 | 0.813295 | 0.626045 | 0.682640 |
| Decision Tree Regressor | 0.724730 | 0.740333 | 0.769368 | 0.724730 |
| Gradient Boosting Regressor | 0.869280 | 0.883137 | 0.871168 | 0.876297 |
| Linear Regressor | 0.628663 | 0.814730 | 0.626075 | 0.682481 |
| Random Forest Regressor | 0.889897 | 0.882924 | 0.899372 | 0.888737 |
Analyze Stacking Ensemble Performance¶
In [54]:
preparedData5["cement 2 water"] = preparedData5["cement"] / preparedData5["water"]
In [55]:
preparedData5.drop("cement", axis=1, inplace=True)
preparedData5.drop("water", axis=1, inplace=True)
In [56]:
bins = [0, 1, 3, 7, 14, 28, 365]
bin_labels = [1, 3, 7, 14, 28, 365]
preparedData5["age-bin"] = pd.cut(x=preparedData5["age"], bins=bins, labels=bin_labels)
In [57]:
preparedData5.drop("age", axis=1, inplace=True)
In [58]:
preparedData5 = pd.get_dummies(preparedData5)
In [59]:
x5 = preparedData5.loc[:, preparedData5.columns != 'strength'] # independent variables
y5 = preparedData5.loc[:, preparedData5.columns == 'strength'] # Target variable
In [60]:
x5train,x5test,y5train,y5test = train_test_split(x5,y5,test_size=0.3,random_state=10)
In [61]:
x5L1, x5L2, y5L1, y5L2 = train_test_split(x5train,y5train,test_size=0.5,random_state=10)
In [62]:
x5L1train, x5L1test, y5L1train, y5L1test = train_test_split(x5L1,y5L1,test_size=0.3,random_state=10)
In [63]:
x5L2train, x5L2test, y5L2train, y5L2test = train_test_split(x5L2,y5L2,test_size=0.3,random_state=10)
In [64]:
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn import tree
from sklearn.ensemble import AdaBoostRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score
In [65]:
models = {}
models["Linear Regressor"] = LinearRegression()
models["Random Forest Regressor"] = RandomForestRegressor(n_estimators = 45, random_state=10)
models["Bagging Regressor"] = BaggingRegressor(n_estimators=45,random_state=10, base_estimator=models["Linear Regressor"])
models["Adaptive Boosting Regressor"] = AdaBoostRegressor( n_estimators=40,random_state=10, base_estimator=models["Linear Regressor"])
y_predictL1 = {}
In [66]:
allPredictions = pd.DataFrame()
for modelName in models.keys():
models[modelName].fit(x5L1train.append(x5L2train, ignore_index=True), y5L1train.append(y5L2train,ignore_index=True))
y_predictL1[modelName] = models[modelName].predict(x5L1test)
allPredictions[modelName] = pd.Series(y_predictL1[modelName].flatten())
allPredictions["Target"] = y5L1test.reset_index(drop=True)
In [67]:
allPredictions
Out[67]:
| Linear Regressor | Random Forest Regressor | Bagging Regressor | Adaptive Boosting Regressor | Target | |
|---|---|---|---|---|---|
| 0 | 37.513163 | 30.503333 | 37.762556 | 37.641856 | 33.30 |
| 1 | 52.782186 | 50.092000 | 52.835272 | 53.283228 | 46.68 |
| 2 | 26.916250 | 26.791556 | 26.891583 | 26.897613 | 20.73 |
| 3 | 28.204639 | 28.722222 | 28.435620 | 29.851639 | 31.03 |
| 4 | 39.586389 | 36.630407 | 39.434324 | 40.205540 | 38.11 |
| ... | ... | ... | ... | ... | ... |
| 103 | 14.674716 | 17.039333 | 14.711353 | 15.433601 | 15.87 |
| 104 | 30.303265 | 29.182667 | 30.393729 | 31.981228 | 33.27 |
| 105 | 22.060262 | 24.087778 | 22.041008 | 22.110590 | 22.14 |
| 106 | 30.983467 | 32.912889 | 31.145475 | 32.776276 | 32.77 |
| 107 | 15.710098 | 15.259556 | 16.007985 | 16.053663 | 10.73 |
108 rows × 5 columns
In [68]:
def bestModel(row):
target = row["Target"]
row.drop("Target", inplace=True)
row = abs(row - target)
row = row.to_dict()
return min(row, key=row.get)
In [69]:
allPredictions.apply(bestModel, axis=1).value_counts()/allPredictions.shape[0]*100
Out[69]:
Random Forest Regressor 62.037037 Adaptive Boosting Regressor 16.666667 Linear Regressor 12.037037 Bagging Regressor 9.259259 dtype: float64
In [70]:
xL2Input = allPredictions.loc[:, allPredictions.columns != 'Target'] # independent variables
yL2Input = allPredictions.loc[:, allPredictions.columns == 'Target'] # Target variable
In [71]:
x5L2test
Out[71]:
| slag | ash | superplastic | coarseagg | fineagg | cement 2 water | age-bin_1 | age-bin_3 | age-bin_7 | age-bin_14 | age-bin_28 | age-bin_365 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 801 | 0.0 | 117.5 | 9.5 | 1022.8 | 753.5 | 1.700229 | 0 | 0 | 0 | 0 | 0 | 1 |
| 772 | 0.0 | 121.6 | 5.7 | 1057.6 | 779.3 | 1.176373 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1022 | 0.0 | 133.6 | 11.1 | 979.5 | 811.5 | 0.800885 | 0 | 0 | 0 | 0 | 1 | 0 |
| 106 | 0.0 | 143.0 | 9.0 | 877.0 | 868.0 | 0.803109 | 0 | 0 | 0 | 0 | 1 | 0 |
| 123 | 0.0 | 174.2 | 11.7 | 1052.3 | 775.5 | 1.380983 | 0 | 0 | 0 | 0 | 1 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 228 | 0.0 | 0.0 | 0.0 | 1012.0 | 830.0 | 1.614583 | 0 | 0 | 0 | 0 | 0 | 1 |
| 697 | 259.7 | 0.0 | 12.7 | 858.8 | 826.8 | 0.906114 | 0 | 0 | 0 | 0 | 1 | 0 |
| 158 | 173.0 | 0.0 | 0.0 | 909.8 | 891.9 | 0.604167 | 0 | 0 | 0 | 0 | 1 | 0 |
| 480 | 0.0 | 126.5 | 5.7 | 860.5 | 736.6 | 1.515975 | 0 | 0 | 0 | 0 | 1 | 0 |
| 509 | 102.0 | 0.0 | 0.0 | 888.0 | 943.1 | 0.796875 | 0 | 0 | 1 | 0 | 0 | 0 |
109 rows × 12 columns
In [72]:
gbr = GradientBoostingRegressor(n_estimators=40,random_state=10)
gbr.fit(xL2Input, yL2Input)
Out[72]:
GradientBoostingRegressor(n_estimators=40, random_state=10)
In [73]:
l2Predictions = pd.DataFrame()
y_predictL2 = {}
for modelName in models.keys():
y_predictL2[modelName] = models[modelName].predict(x5L2test)
l2Predictions[modelName] = pd.Series(y_predictL2[modelName].flatten())
l2Predictions["Target"] = y5L2test.reset_index(drop=True)
In [74]:
gbr_y_predict = gbr.predict(l2Predictions.drop("Target", axis=1))
In [75]:
r2_score(l2Predictions["Target"], gbr_y_predict)
Out[75]:
0.793510776004939
Tune Gradient Boosting Regressor Hyperparameters¶
In [76]:
gradient_boost_parameters = {'learning_rate': [0.01,0.02,0.03,0.04],
'subsample' : [0.9, 0.5, 0.2, 0.1],
'n_estimators' : [20, 50, 100, 200, 500, 1000, 1500, 2000],
'max_depth' : [3,6,9,12,15,18,21]
}
In [77]:
gbr = GradientBoostingRegressor(random_state=10)
grid_gbr = GridSearchCV(estimator=gbr, param_grid = gradient_boost_parameters, cv = 4, n_jobs=-1)
gbr_result = grid_gbr.fit(x2train, y2train)
print("Best: %f using %s" % (gbr_result.best_score_, gbr_result.best_params_))
Best: 0.924573 using {'learning_rate': 0.02, 'max_depth': 6, 'n_estimators': 2000, 'subsample': 0.1}
In [87]:
gbr = GradientBoostingRegressor(learning_rate=0.02, subsample=0.1, n_estimators=2000, max_depth=6, random_state=10)
In [88]:
cvResultsOptimized = modelTraining2.performNumericalCrossValidation(gbr, x2train, y2train, 4, "Optimized Gradient Boosting Regressor")
cvResultsOptimized
Out[88]:
| Model Name | Fold Number | Mean Absolute Error | Root Mean Squared Error | R Squared | |
|---|---|---|---|---|---|
| 0 | Optimized Gradient Boosting Regressor | 1 | 3.272959 | 4.386829 | 0.936685 |
| 1 | Optimized Gradient Boosting Regressor | 2 | 3.395844 | 4.641592 | 0.927584 |
| 2 | Optimized Gradient Boosting Regressor | 3 | 3.219891 | 4.701529 | 0.902560 |
| 3 | Optimized Gradient Boosting Regressor | 4 | 3.312583 | 4.578769 | 0.931463 |
In [89]:
performanceStats = cvResultsOptimized.drop("Mean Absolute Error", axis=1).drop("Root Mean Squared Error", axis=1).groupby('Model Name').describe()
performanceStats
Out[89]:
| R Squared | ||||||||
|---|---|---|---|---|---|---|---|---|
| count | mean | std | min | 25% | 50% | 75% | max | |
| Model Name | ||||||||
| Optimized Gradient Boosting Regressor | 4.0 | 0.924573 | 0.015141 | 0.90256 | 0.921328 | 0.929524 | 0.932768 | 0.936685 |
In [99]:
print("Percent improvement due to hyperparameter optimization: " + "{:.2f}".format(100 * (0.924573-0.883137) / 0.883137))
Percent improvement due to hyperparameter optimization: 4.69
In [90]:
print("95% R Squared Confidence Interval: " + "{:.3f}".format(performanceStats.iloc[0,1]-performanceStats.iloc[0,2]*1.96)
+ " -- " + "{:.3f}".format(performanceStats.iloc[0,1]+performanceStats.iloc[0,2]*1.96))
95% R Squared Confidence Interval: 0.895 -- 0.954
Tune Random Forrest Regressor Hyperparameters¶
In [94]:
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 200, stop = 2000, num = 10)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(10, 110, num = 11)]
max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 4]
# Method of selecting samples for training each tree
bootstrap = [True, False]
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf,
'bootstrap': bootstrap}
In [96]:
rfr = RandomForestRegressor(random_state=10)
rfr_random_search = RandomizedSearchCV(estimator = rfr, param_distributions = random_grid, n_iter = 100, cv = 4, random_state=10, n_jobs = -1)
rfr_result = rfr_random_search.fit(x2train, y2train)
print("Best: %f using %s" % (rfr_result.best_score_, rfr_result.best_params_))
Best: 0.885420 using {'n_estimators': 200, 'min_samples_split': 2, 'min_samples_leaf': 1, 'max_features': 'auto', 'max_depth': 60, 'bootstrap': True}
In [97]:
rfr = RandomForestRegressor(random_state=10, n_estimators=200, min_samples_split=2, min_samples_leaf=1, max_features="auto", max_depth=60, bootstrap=True)
In [98]:
cvResultsOptimized = modelTraining2.performNumericalCrossValidation(rfr, x2train, y2train, 4, "Optimized Random Forest Regressor")
cvResultsOptimized
Out[98]:
| Model Name | Fold Number | Mean Absolute Error | Root Mean Squared Error | R Squared | |
|---|---|---|---|---|---|
| 0 | Optimized Random Forest Regressor | 1 | 3.893972 | 5.108293 | 0.914146 |
| 1 | Optimized Random Forest Regressor | 2 | 3.733208 | 5.155902 | 0.910647 |
| 2 | Optimized Random Forest Regressor | 3 | 4.086786 | 5.835058 | 0.849911 |
| 3 | Optimized Random Forest Regressor | 4 | 4.357615 | 6.378990 | 0.866975 |
In [100]:
performanceStats = cvResultsOptimized.drop("Mean Absolute Error", axis=1).drop("Root Mean Squared Error", axis=1).groupby('Model Name').describe()
performanceStats
Out[100]:
| R Squared | ||||||||
|---|---|---|---|---|---|---|---|---|
| count | mean | std | min | 25% | 50% | 75% | max | |
| Model Name | ||||||||
| Optimized Random Forest Regressor | 4.0 | 0.88542 | 0.031952 | 0.849911 | 0.862709 | 0.888811 | 0.911522 | 0.914146 |
In [101]:
print("Percent improvement due to hyperparameter optimization: " + "{:.2f}".format(100 * (0.88542-0.882924) / 0.882924))
Percent improvement due to hyperparameter optimization: 0.28
Gradient Boosting Regressor Production Model Test Results¶
In [91]:
productionResults = pd.DataFrame(columns = ["Mean Absolute Error", "Root Mean Squared Error", "R Squared"])
productionModel = GradientBoostingRegressor(learning_rate=0.02, subsample=0.1, n_estimators=2000, max_depth=6, random_state=10)
productionModel.fit(x2train, y2train)
y_predict = productionModel.predict(x2test)
# Mean Absolute Error
mae = mean_absolute_error(y2test, y_predict)
# RMSE
rmse = mean_squared_error(y2test, y_predict)**0.5
# R2 Squared:
r2 = r2_score(y2test, y_predict)
new_row = {"Mean Absolute Error" :mae, "Root Mean Squared Error":rmse, "R Squared": r2}
#append row to the dataframe
productionResults = productionResults.append(new_row, ignore_index=True)
productionResults
Out[91]:
| Mean Absolute Error | Root Mean Squared Error | R Squared | |
|---|---|---|---|
| 0 | 3.137745 | 4.51065 | 0.922955 |
Summary of Results¶
- The Optimized Gradient Boosting Regressor (model) accurately predicts concrete strength with 95% R Squared Confidence Interval of 0.895 -- 0.954 based on cross validation on training data.
- Comparing an average R Squared value of the model on training data of 0.923 with the 0.923 value on testing data indicates the model has generalized well, neither underfitting nor overfitting.
- Hyperparameter tuning of the Gradient Boosting model improved performance by 4.69%
- Hyperparmeter tuning of the Random Forest model only improved performance by 0.28%
- Graident Boosting model is the best choice for predicting the strength of concrete because there is less variance in its predictions and the hyperparameter optimization enables it to perform better on average than the Random Forest model.
- Significant performance improvements can be gained through feature engineering for some models. For example, the R Squared value for the Linear Regression model improves from 0.629 to 0.815 by creating two new features ( cement/water and age bins).
- The models that performed the best without any feature modeling (Gradient Boosting and Randform Forest) did not enjoy a significant benefit from feature engineering.
- The performance improvement from single feature engineering as opposed to multiple feature engineering was not nearly so significant. The performance improvement from cement/water plus age bins was not the sum of their indvidual performance contributions, it was much higer. This requires further analysis to understand.
- Using the Stacking ensemble technique lead to a model that performed better than the weaker of the models (Linear Regression, Adaptive Boosting, Bagging, Decision Tree) but not as strong as the best single model predictors (Gradient Boosting and Random Forest).
- When using the Stacking ensemble model, the "expert" first level models had inbalanced performance with Random Forest being the best for 62% of the predictions. One assumes that stacking performance improves when there is a more balanced distribution contribution of predictions by all models but this intuition needs to be validated.
- Visualization of model performance using boxplots led to the disovery of differences in standard deviation between Gradient Boosting and Random Forest preditors.
- Because the business requirement was to be above 0.85 for R squared, cross validation was very helpful to determine the performance range of models. Using 95% confidence interval for model performance disqualified Random Forest from use because its lower bound for performance is less than 0.85. Note that even for one of its cross validation folds, it scored slightly less than 0.85.
- The polynomial degree versus error graph helped illustrate the problem that as the degree increases, the error as measured against test sets increases. Since it's not possible to compare its performance against the other models using R squared, error metrics like RMSE were used. The polynomial model of degree 2 had more error than Gradient Boosting and Random Forest.
- The many possible alternatives for model types, hyperparameters, and feature engineering, finding the best solution requires trying many combinations of them. Reusable code, like that offered by the ExploratoryDataAnalysis and ModelTraining classes, can greatly improve the efficiency of working through the data science lifecycle.
- Pipelines were not used due to slight differences in the features under consideration and the limited value of their reuse.
- Feature scaling was not as the model performance results were reasonable and sufficient for comparison. Due to how scaling changes datatypes (dataframe to Numpy array), applying scaling would have required additional coding and modifications to my reusable classes but there was no time to do that work.